martes, 28 de mayo de 2013

Conectiva lógica


En lógica, una conectiva lógica, o simplemente conectiva, es un símbolo que se utiliza para conectar dos fórmulas, de modo que el valor de verdad de la fórmula compuesta dependa del valor de verdad de las fórmulas componentes.

En programación se utilizan para combinar valores de verdad y obtener nuevos valores que determinen el flujo de control de un algoritmo o programa.
Las conectivas lógicas son, junto con los cuantificadores, las principales constantes lógicas de muchos sistemas lógicos, principalmente la lógica proposicional y la lógica de predicados.

Conectivas

Las conectivas son funciones de verdad. Quiere decir que son funciones que toman uno o dos valores de verdad, y devuelven un único valor de verdad. En consecuencia, cada conectiva lógica puede ser definida mediante una tabla de valores de verdad que indique qué valor devuelve la conectiva para cada combinación de valores de verdad. A continuación hay una tabla con las conectivas más usuales y su definición mediante tablas de verdad:
Conectiva Notación Ejemplo
de uso		 Análogo
natural		 Ejemplo de uso en
el lenguaje natural		 Tabla de verdad
Negación 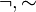\neg,\sim \, \neg p \, no No está lloviendo. \begin{array}{c||c} \phi & \neg \phi \\ \hline 1 & 0 \\ 0 & 1 \\ \end{array}
Conjunción \and,\And, \cdot \, p \and q \, y Está lloviendo y es de noche. 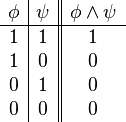\begin{array}{c|c||c} \phi & \psi & \phi \and \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array}
Disyunción \or \, p \or q \, o Está lloviendo o es de noche. \begin{array}{c|c||c} \phi & \psi & \phi \or \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \\ \end{array}
Condicional material 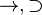\to,\supset p \to q \, si... entonces Si está lloviendo, entonces es de noche. 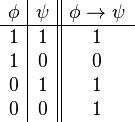\begin{array}{c|c||c} \phi & \psi & \phi \to \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\ \end{array}
Bicondicional \leftrightarrow, \equiv \, p \leftrightarrow q \, si y sólo si Está lloviendo si y sólo si es de noche. \begin{array}{c|c||c} \phi & \psi & \phi \leftrightarrow \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}
Negación
conjunta		 \downarrow \, p \downarrow q \, ni... ni Ni está lloviendo ni es de noche. \begin{array}{c|c||c} \phi & \psi & \phi \downarrow \psi \\ \hline 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}
Disyunción
excluyente		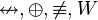 \nleftrightarrow, \oplus, \not\equiv, W p \nleftrightarrow q \, o bien... o bien O bien está lloviendo, o bien es de noche. 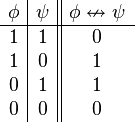\begin{array}{c|c||c} \phi & \psi & \phi \nleftrightarrow \psi \\ \hline 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \\ \end{array}
a la/s
Etiquetas:

No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)